힙이란?
- 힙(heap)을 사용해 정렬하는 알고리즘
- 힙은 '부모의 값이 자식보다 항상 크다(우선순위가 높다)'는 조건을 만족하는 완전이진트리
- 부모의 값이 자식보다 항상 작아도 힙이라고 함(부모와 자식 요소의 관계만 일정하면 됨)
- 우선순위 큐(Priority Queue)가 힙 자료구조를 이용해 구현됨
👆 완전이진트리
부모는 자식을 왼쪽부터 추가하며(완전), 부모가 가질 수 있는 자식의 개수가 최대 2개(이진)인 트리
완전이진트리 → 힙 전환
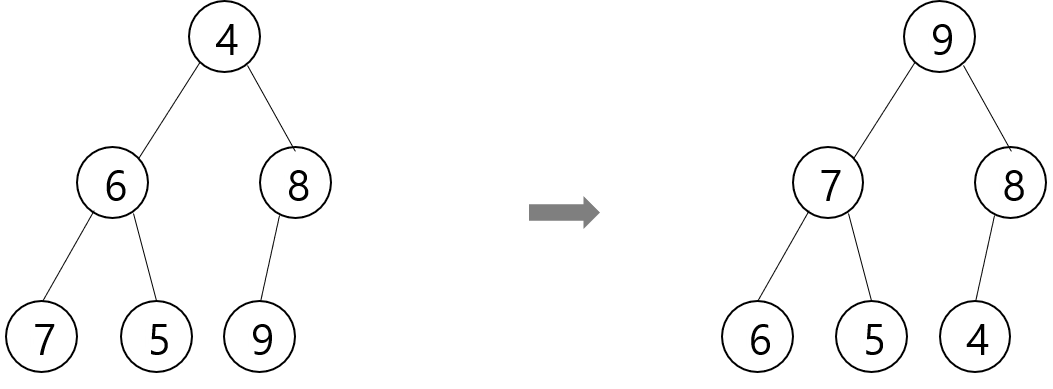
- 힙은 루트가 가장 큰(혹은 작은) 값이어야 함
- 즉, 모든 부모와 자식의 관계는 항상 부모의 값 >= 자식의 값이 성립되어야 함
- 힙에서 부모와 자식 관계는 일정하지만 형제 사이의 대소 관계는 일정하지 않음
힙의 요소를 배열에 저장
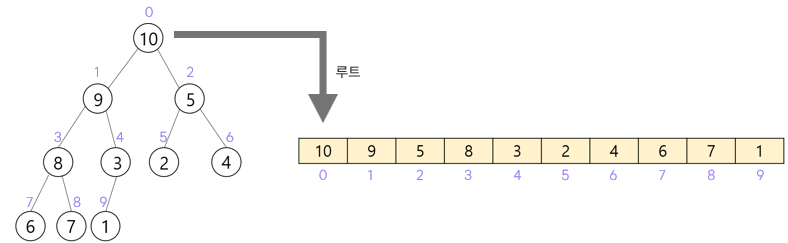
힙의 요소를 배열에 저장하면 부모와 자식의 인덱스 사이에는 다음과 같은 관계 성립
1. 부모는 a[(childIdx - 1) / 2]
2. 왼쪽 자식은 a[parentIdx * 2 + 1]
3. 오른쪽 자식은 a[parentIdx * 2 + 2]
힙 정렬
- '가장 큰(우선순위가 높은) 값이 루트에 위치'하는 특징을 이용하는 정렬 알고리즘
- 힙에서 가장 큰 값인 루트를 꺼내는 작업을 반복하고 그 값을 늘어놓으면 배열의 정렬 종료
- 힙 정렬은 선택 정렬을 응용한 알고리즘이며 힙에서 가장 큰 값인 루트를 꺼내고 남은 요소에서 다시 가장 큰 값을 구해야 함
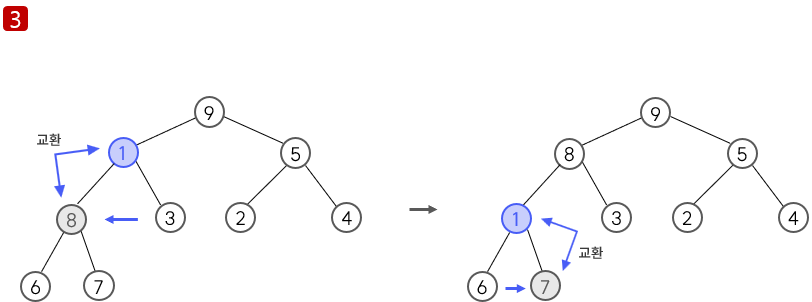
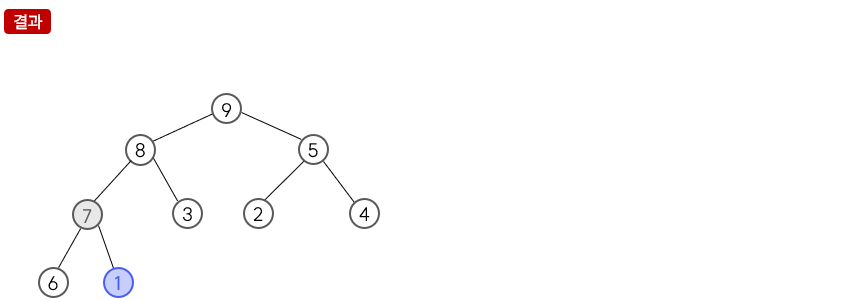
루트 제거 후 힙 상태 유지
1. 루트를 꺼낸다.
2. 마지막 요소를 루트로 이동시킨다.
3. 자기보다 큰 값을 가지는 자식 요소(두 자식 요소 중 더 큰 값을 가지는 자식과 비교)와 자리를 바꾸며 아래쪽으로 내려가는 작업을 반복한다. 자식의 값이 더 작거나, 더 이상 비교할 자식이 없는 경우 작업이 종료된다.
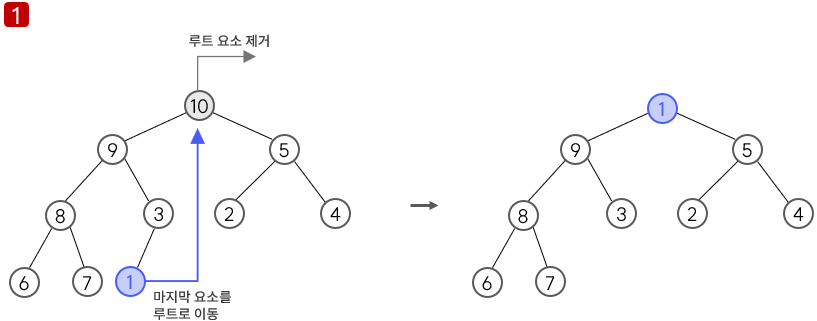
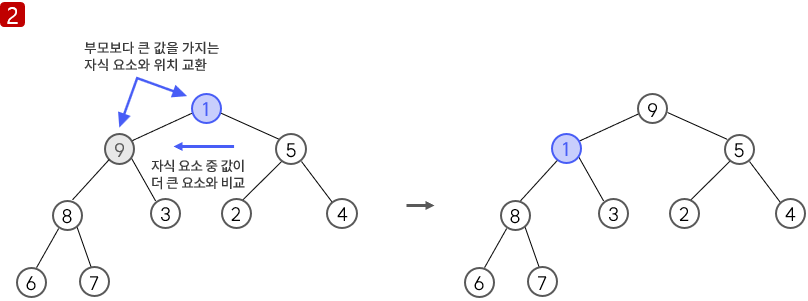
힙 정렬 알고리즘
- 배열을 사용해 힙 정렬 알고리즘을 구현하기 위해서는 우선 배열을 힙 상태로 초기화해야 함
- " 힙의 루트 노드를 배열의 마지막 요소와 교환 -> 남은 요소들을 다시 힙 상태로 정렬 " 의 과정을 반복하는 정렬 알고리즘
- 힙 정렬의 시간 복잡도는 O(log n)
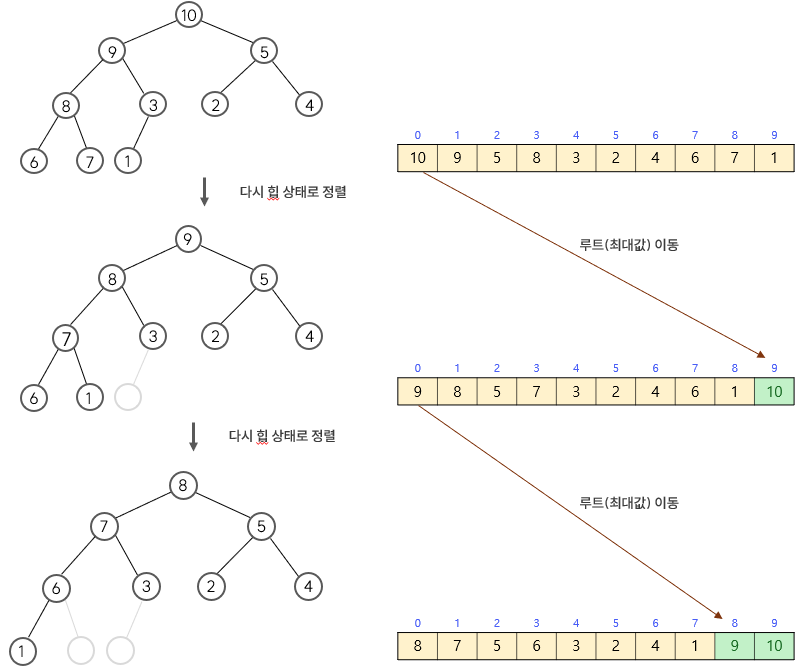
... 이하 생략...
'Algorithm > 06. 정렬' 카테고리의 다른 글
| 정렬 알고리즘 정리 (0) | 2025.12.28 |
|---|---|
| 6-9. 도수 정렬(Counting Sort) (0) | 2021.06.25 |
| 6-7. 병합 정렬(Merge Sort) (0) | 2021.05.03 |
| 6-6. 퀵 정렬(Quick Sort) (0) | 2021.03.11 |
| 6-5. 셸 정렬(Shell Sort) (0) | 2021.02.28 |